Science
The Strange Truth About Alternative Facts
Now if a single moral judgment depends on a unit of analysis, then surely a political philosophy that imagines some sort of societal structure that maximizes some moral values (whatever they may be), must also depend on a unit of analysis.

Facts are overrated in political and moral debates. They’re fragile and impotent. They don’t do the work expected of them. What follows is an explanation of why no one should be persuaded by most facts. This is not a rehashing of the well-known inability of facts to persuade emotional beings. Nor is it a postmodern denial of truth. My point is that facts which are absolutely true can be absolutely irrelevant in overlooked ways.
It’s obvious that facts can be irrelevant; everyone knows that. But some facts that seem relevant are not. For example, let’s say you ask me whether or not women face gender bias in grad school admissions and I tell you that hummingbirds can fly backwards. This is an obviously irrelevant fact. But if I told you that data shows female applicants were significantly less likely than male applicants to be accepted to grad school, that would also be irrelevant. How could that fact possibly be irrelevant? It seems like exactly the kind of fact that could help answer the question. But the fact is at the wrong scale; its unit of analysis is wrong, which makes it irrelevant. This requires some explanation…
The term ‘unit of analysis’ comes from the quantitative social sciences. It refers to the specific type of thing a scientist wants to measure and compare. For example, an economist comparing the GDP of Mexico to the GDP of Japan is using ‘country’ as his unit of analysis. A psychologist conducting a controlled experiment is taking a ‘treatment group’ as his unit of analysis.
The unit of analysis is not to be confused with the unit of observation, which is the unit described by one’s data. For example, a study may have a unit of observation at the individual level but may have a unit of analysis at the neighborhood level, drawing conclusions on neighborhood characteristics from data collected from individuals.
When two scientists choose two different units of analysis, they may come to apparently opposite conclusions, both of which are true. In applied statistics, this is known as Simpson’s paradox. One of the best-known examples of Simpson’s paradox is a study of gender bias among graduate school admissions at University of California, Berkeley. The admission figures for the fall of 1973 showed that men applying to the university were more likely than women to be admitted. However, it was found that men were not more likely than women to be admitted by the academic departments which make up the university. This is explained by the fact that women tended to apply to departments with low rates of admission among qualified applicants (such as the English Department), whereas men tended to apply to departments with high rates of admission among qualified applicants (such as engineering and chemistry).
This table shows a simplified version of how that can work:
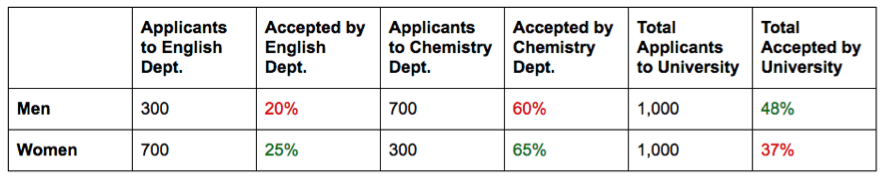
In this example, the statement ‘men are more likely to be accepted’ is true, taking ‘university’ as the unit of analysis. At the same time, given the same data, the statement ‘women are more likely to be accepted’ is true, taking ‘department’ as the unit of analysis. These are literally alternative facts. Both statements are true, but which is more relevant? That depends on the question the facts are meant to answer. A question about the university as an indivisible whole calls for one correct answer, while a question about the departments calls for the opposite correct answer. So the real question is, what’s the right question? Since nobody applies to the university as an indivisible whole, the right question is about the departments, and so the relevant fact is that women are admitted at a higher rate than men. The fact that women are admitted to the university at a lower rate than men is irrelevant.
Now we see that the question must specify a unit of analysis if we want a coherent answer. The same is true of questions asked in moral and political philosophy. What kind of society is most fair, or most safe, or most just, or most beneficial, or most free? No matter which question one sets out to answer, the question must specify a unit of analysis. Most fair for whom? For people. But for people at which scale? For individuals, or for families, or for neighborhoods, or for genders, or races? Simpson’s paradox implies that two philosophers who ask the same question with different units of analysis will sometimes come to opposite conclusions.
If one were to make moral judgments about the admissions at Berkeley, for example, conclusions would depend on the units of analysis chosen as units of moral agency and the unit of moral harm. Suppose we take the ‘individual’ to be the unit of moral harm. Then we care about outcomes for individuals, and individual applicants only apply to single departments, so we will look for evidence of departmental treatment of applicants, and find no bias against women. Or suppose we take gender as the unit of moral harm. Then we have an array of contradictory units of moral agency from which to choose. Is the whole of the university an agent that produces an outcome (bias against women)? Or are the departments' agents which each produce their own outcomes (no bias against women)? Or maybe we decide that a societal system of male bias is the relevant agent, which should be counteracted by a system of localized female bias in the university. Each of these a priori units of analysis leads to different conclusions about the moral character of grad school admissions at Berkeley.
Now if a single moral judgment depends on a unit of analysis, then surely a political philosophy that imagines some sort of societal structure that maximizes some moral values (whatever they may be), must also depend on a unit of analysis.
As we have seen, apparently conflicting conclusions can all be correct, given different a priori units of analysis. But is there such a thing as a correct unit of analysis? Philosophers have used state, economic class, gender, individual, race, neighborhood, and many other units. And there are practically infinitely many more ways in which it is possible to group people for analysis. The choice of unit is a choice between an infinite number of options. I have argued elsewhere that ‘individual’ is the only correct unit of moral analysis. But here, my goal is just to show that true facts are irrelevant if their units of analysis are wrong, and since there are so many possible units of analysis, a person with an opinion should have a good reason for choosing one unit over the others.
Citing true facts is child’s play. If you’re interested in moving from facts to Truth, you need a good reason to believe your facts are relevant, which means you need a good reason to believe your questions are relevant.





